|
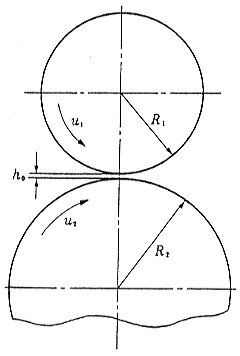
ID-S46 転がり軸受の弾性流体潤滑とはどのようなものか 転がり軸受の中の転がり接触面に、弾性流体潤滑によって油膜ができているといわれます。弾性流体潤滑とは、どのようなものでしょうか? 転がり軸受を静定格荷重の近くまで負荷すると、軸受の中の転動体と軌道との間の面圧は大きな値になります。Hertzの弾性接触理論によって計算すると、その面圧は4GPa程度(1GPa=10,000kgf/cm2=100kgf/ cm21万気圧)の大きさになり、転動体と軌道には転動体直径の1/10,000の圧痕すなわち永久変形がおこります。この程度までの大きな面圧を受けながら、軸受を使っても、潤滑さえ十分であれば、転がり接触面が損傷をおこすことは少ないことが経験されてきました。 このような経験的事実を理論的に説明したのが弾性流体潤滑(Elasto-hydrodynamic Lubrication=EHL)理論です1) 2)。そして、最近ではEHLを軸受の設計と応用技術の指針とするようになっています。EHLに至る考え方を以下に示します。 ●転がり接触面の弾性変形を採りいれる 転がり軸受の中の転動体と軌道との間の接触は、玉軸受では点接触、ころ軸受では線接触になる。簡単のために、ここでは線接触をとり上げます。 図1に示すような2円筒の転がり接触の状態を等価に置き換えて、図2のような円筒と平面の間の転がり接触とすることができます。
その場合、  のようになります。 これを、Reynoldsの流体潤滑の基礎方程式に適用し、Gatcombeの境界条件を用いると、紙面に垂直な単位幅当りの負荷容量Wは、  のように表わされます。hoは最小油膜厚さ、ηは潤滑油の粘度です。 この式を使って、円筒ころ軸受のころと軌道との間の転がり接触面に形成される流体潤滑油膜の厚さhoを計算すると、普通に使われる運転条件では1/100〜1/1,000μmのオーダにしかなりません。この値は、転がり接触する表面粗さより、はるかに小さいです。 それに比べて、この転がり接触面に生ずる弾性変形の程度は接触面の幅1mm、接近量で10μm程度にもなることがあります。前記の流体潤滑理論では、接触面を鋼体としているので、この接触面の弾性変形を考えにいれなければなりません。 ●潤滑油の高圧粘度をとりいれる 転がり軸受のように、接触面圧が4GPa程度までの高圧の下で潤滑油を使う場合には、潤滑油の高圧粘度を考えなければなりません。 一般に圧力が高くなるほど、液体の粘度は高くなることが知られています。潤滑油についても、古くから最高圧力1GPa程度までの高圧での粘度と密度の測定が行なわれています。 一般には、高圧の下での鉱油系潤滑油の粘度ηは、大気圧の下での粘度η0に比べて、次の式で近似的に表わされています。  pは圧力、αは粘度の圧力係数と呼ばれる定数で、鉱油では20(GPa)-1程度の値です。 図3に、石油系潤滑油の圧力による粘度の増加の一例を示しました3)。図のように、1GPaのような高圧の下では、粘度は数桁も高くなることがわかります。  図3 圧力による潤滑油の粘度の増加 ●EHLとは EHL理論は、流体潤滑に加えて、接触面の弾性変形と高圧による潤滑油の粘度の増加をとりいれたものです。すなわち、Reynoldsの流体潤滑の基礎方程式にHertzの弾性変形理論、そして式(4)の圧力と粘度の関係を連立させて解を求めます。しかし、方程式が複雑になるために、解析解を求めるのは不可能です。そこで、数値計算をして、図4のような計算結果が得られています4)。 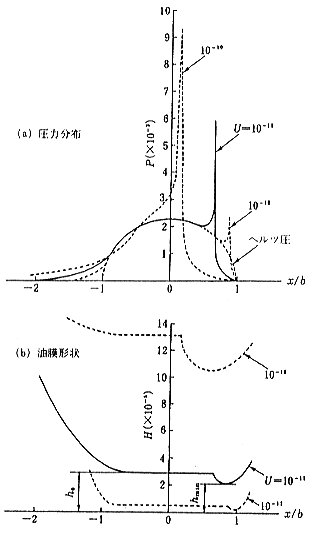 図4 EHLによる圧力分布と油膜性状 G=5000、W=3×10-15 図をみると、接触面の圧力分布は、全体としては、Hertzの弾性接触理論から導かれる半楕円に似ています。左側の入口では、くさび形状の流体膜による圧力上昇、右側の出口では圧力スパイクと呼ばれるピークができます。 流体膜の形状は、膜厚はほぼ一様で、出口側で圧力スパイクに応じた位置で薄い油膜にくびれています。ここで膜厚は最小値hminになります。 そして、この最小油膜厚さhminは、Dowson-Higginsonによると次の式で表わされます。  ここで、  この記号は、前述の説明に用いたものと同じですが、E’は等価弾性係数で、次の式で表わされます。  Eは縦弾性係数、vはポアソン比である。 このEHLによる最小油膜厚さは、式(3)の古典論から求められる値に比べて数10〜数100倍の大きさになり、マイクロメートルのオーダになります。これは、現在の超精密加工によって得られている転動体と軌道の表面粗さよりも大きな値です。したがって、転がり軸受の中で、EHLによる油膜の形成により、転がり運動する表面が非接触の状態になることを推定させます。 さらに重要なことは、古典論では、式(3)のように、ho∝W-1であったのが、EHLではhmin∝W-0.13になり、EHLの油膜厚さは荷重の影響をあまり受けないという結果が得られたことです。 ●最近のEHLは 以上述べたEHLは線接触についてです。その後、玉軸受のような点接触の転がり接触面についてのEHLも研究され、油膜厚さと圧力分布が3次元的に求められています。 そして、理論と実験との対比も多くの研究によってなされ、圧力スパイクの存在も、理論値よりは小さいが実証されています。 さらに最近では、接触面入口部分の温度上昇、グリース潤滑を考えにいれたEHL、油不足条件下のパーシャルEHL、さらに表面粗さの凹凸形状まで考えたマイクロEHLにまで発展をつづけています。 |
「参考文献」
| ||||||||||
Copyright 1999-2003 Japan Lubricating Oil Society. All Rights Reserved.